Graphs
In mechanics graphs can be used to great affect. There are four main types of graphs you will need to be able to construct and interpret Velocity-Time graphs, Speed-Time graphs, Displacement-Time graphs and Distance-Time graphs.
·
For velocity-time graphs the gradient
= acceleration and the area under the curve = displacement
·
For speed-time graphs the area under the
curve = distance
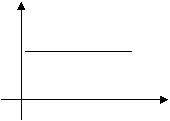
Constant Velocity
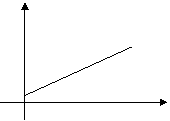
Constant Acceleration
·
For displacement-time graphs the gradient
= velocity
·
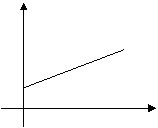
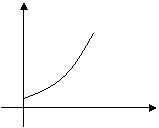
For distance-time graphs the gradient
= speed
Constant Velocity
Constant Acceleration
Distance-time graph
Example
A cyclist was riding in the park at a constant speed of 3 ms-1 for 12 seconds until he came to a stop for 15 seconds to catch his breath. He then rode back to the entrance in 10 seconds. Calculate his speed during the third stage of his journey by plotting a distance-time graph.
The first step is to draw a distance-time graph.
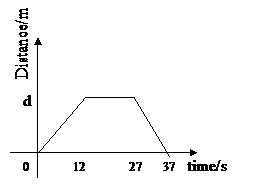
Now using the information provided for the first stage of the journey it is possible to calculate d.
Gradient = speed
3 = ![]() d = 36 m
d = 36 m
It took him 10 seconds to ride back to the entrance. We now using this information need to calculate his speed.
Speed = ![]() ms-1
ms-1
Vectors
When two forces act on an object it is important which direction these forces
are acting. These forces can often be resolved to find a resultant vector which
describes the subsequent movement of the body.
3N 5N
![]()
8N
Example
The following two forces can be resolved using the triangle method or
the parallelogram method.
 |
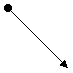
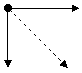
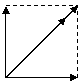
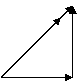
Note that vector diagrams always use arrows for forces and the resultant force is represented using a double arrow.
Parallelogram method
 |
Triangle method
 |
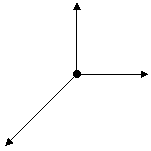
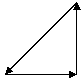
Vector Triangle
When there is no resultant force a vector triangle can be used to show
the body is at equilibrium.
 |
|||
 |
|||
Resolving Vectors
In the same way that two vectors can be represented as one resultant vector,
it is possible to resolve one vector into two components both at right angles.
This is used in particular in the next section concerning projectiles.
