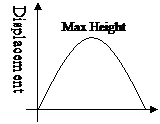Equations of Motion

The following equations only apply to motion in a straight line with constant acceleration. Physics models are often employed to provide these conditions, for example questions often consider air resistance negligible.

v = u + at

 s = (u + v)t
          2

s = ut + ½at²

v² = u² + 2as

 

Where  v = final velocity
            u = initial velocity
            u = displacement
            a = acceleration
            t = time

Note that you only need to learn the first two equations, and in actual fact the first equation is that same as acceleration = change in velocity
time 

 

A simple example

A ball is dropped from a height of 20m with what speed does it hit the ground.
Acceleration due to gravity = 9.81 ms^-2 and air resistance is negligible.

The first step is to list what we know and what we want. The question states that he dropped the ball so its initial velocity was zero. We also know the acceleration and the distance and want to find the final velocity.

u = 0    v = ?    s = 20  a = 9.81     t = unknown and not needed

We should therefore choose the equation that omits time.

v² = u² + 2as
v²= 0 + 2 x 9.81 x 20
v = 19.8 ms^-1

 

The parachutist

For all of the above examples it has been considered that air resistance is negligible, however as we know this isn’t really the case.

Before Falling
Acceleration = 9.81ms^-2, the resultant force is zero and the velocity is zero

When the object begins to fall
Air resistance acts upwards, the resultant force equals the weight minus air resistance and acceleration decreases

As velocity increases
The resistive force (air resistance) increases until air resistance equals weight and therefore the resultant force is zero and acceleration is zero. This is known as terminal velocity.

When the parachute opens
Air resistance increases dramatically so that air resistance is greater than the force due to weight. The acceleration is negative (the person decelerates) until they reach a new lower terminal velocity.

 

 

Extended

More complex questions involve motion in a curved path, normally involving some sort of projectile. For these questions the horizontal and vertical components of velocity are separated.

A plot of a ball being thrown including key points.

 

 

Max Height Vertical Velocity = 0
Max Horizontal Distance Vertical Displacement = 0
Range = Horizontal Displacement
Horizontal Acceleration = 0
Vertical Acceleration = -9.81 ms^-2

 

Example

A ball is thrown at 30 degrees to the horizontal with an initial velocity of 10 ms^-1 and lands in 0.510 seconds, what is the ball’s range to 2 s.f. (take acceleration as 9.81 ms^-2 and air resistance is negligible)?

 

Now we need to work of the components of velocity:

 Initial Vertical Component of Velocity
10 Sin(30) = 5.00

 Initial Horizontal component of Velocity
10 Cos(30) = 8.66

Using horizontal components of velocity it is know that acceleration is zero, we can therefore apply the equations of motion:
t = 0.510    s = ?    a = 0    u = 8.66  

s = ut + ½at²
s = (8.66 x 0.510) + (½ x 0 x 0.510²)
s = 4.4 m to 2 s.f.

 

Graphs of projectiles