Deformation of Solids

Hooke’s law
The amount by which an object is stretch is proportional to the amount of force applied, assuming the elastic limit has not been exceeded. An object stretched beyond its elastic limit will become permanently deformed.

 

 

 

 

 

 

Hooke’s Law (as long as the elastic limit has not been exceeded)

Force = Extension x Spring Constant                                                           

Spring Constant (Nm^-1)

 

Equations

Stress =            Force           
              Cross sectional Area                                                                        

Stress (Nm^-2 or Pa)                                                                                                                  

 

Strain =      Extension    
              Original Length                                                                                

Strain (None)

Young Modulus =   Stress
                               Strain

Young Modulus (Nm^-2 or Pa)

 

Graphical Solutions

 

 

 

 

 

 

Gradient = Young Modulus

 

 

 

 

 

Gradient = Spring Constant

Strain Energy/Kinetic Energy/Work = Area

 

Young Modulus =  Gradient x Length
                            Cross Sectional Area

 

Elastic and plastic materials

Elastic                                                                         

 

 

 

 

 

An elastic material returns to its original size and shape when the load is removed e.g. rubber.

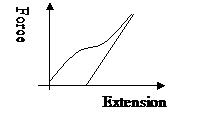Plastic

 

 

 

 

A plastic material fails to return to its original size and shape when the load is removed and shows permanent strain e.g. polythene.

 

Brittle and Ductile materials

 

Brittle                                                                              

 

 

 

 

 

A brittle material shows elastic behaviour up until its breaking point with stress directly proportional to strain.

Ductile

 

 

 

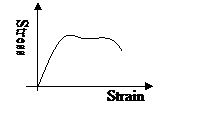A ductile material stretch proportional to the stress up until a point where the wire stretches more and more and will not return to its original length. Plastic deformation.

 

 

Spring Combinations

 

 

 

 

 

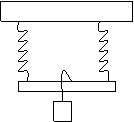Half the extension
Double the spring Constant

 

 

 

 

 

 

Double the extension
Half the spring Constant

 

Experiment to give the Young Modulus of a wire.

Note this is the only experiment that could be asked about in the exam.

 

Measurements

Diameter of wire           Micrometer in several places and an average used
Length of wire              Meter rule for a wire greater than 1 meter
Mass                            Repeat on unloading as well as loading to ensure the material doesn’t exceed its elastic limit
Extension                      Vernier scale repeated on loading/unloading and a mean used

 

 

 

 

 

 

 

 

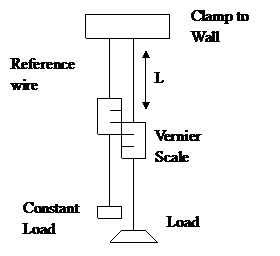Calculations

The following will need to be calculated:

 Cross sectional area      =  π(d/2)² 

Force                           =  Mass x 9.81

 Stress                           =  Force
                                         Area

 Strain                           =      Extension
                                        Original Length

 

Final step
Plot a stress-Strain graph and draw a line of best fit. Calculate the gradient using a tangent to give the Young Modulus.